
Nedávno se objevila zpráva, že by nás balóny plněné héliem mohly vynést až na okraj vesmíru. Připadá vám to střeštěné. Já to pokládám za nesmysl a dokážu vám proč.
Dalibor Šrámek v komentářích pod svým článkem Budeme létat do vesmíru héliovým balónem? v reakci na pochybnosti o realizovatelnosti takového nápadu napsal:
Vzhledem k tomu, že se tím údajně zabývají 20 let, tak doufám, že si aspoň nějaké předběžné výpočty udělali.
Oni si je jistě udělali, ale jednoduchý výpočet toho, do jaké výšky vyletí balón si můžeme snadno udělat i my.
Nebojte se rovnic
Vystačíme si s tím, co by měl znát každý průměrný středoškolák – tzn. se stavovou rovnicí pro ideální plyn, výpočty s látkovým množstvím (moly a tak :-) a vztahy pro výpočet objemů a povrchů jednoduchých těles.
Jak velký bude vztlak?
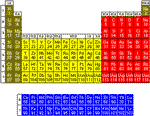
Víme, že stejný počet molekul jakéhokoliv množství plynu zaujme za stejných podmínek stejný objem. Z periodické tabulky prvků zjistíme, kolik váží jeden mol hélia a dusíku. Hélium proto, že bude náplní balónu a dusík jsem si zvolil proto, že je v atmosféře nejhojnější a leží v tabulce mezi uhlíkem a kyslíkem, které jsou také hojné.
Hélium je netečný plyn, a proto netvoří sloučeniny a vyskytuje se pouze v jednoatomových molekulách. Proto hmotnost jednoho molu héliového plynu rovnou odečteme z periodické tabulky – cca 4 g/mol.
Dusík se vyskytuje ve dvouatomových molekulách, a tak hodnotu uvedenou v periodické tabulce musíme vynásobit dvěma a získáme – cca 28 g/mol.
Notoricky známý Archimédův zákon nám říká, že “těleso ponořené do kapaliny nadlehčováno jest silou rovnající se tíze kapaliny jím vytlačené”. Z toho pro nás plyne, že když ponoříme 1 mol hélia uzavřený v balónu do dusíku o stejném tlaku a teplotě, bude nadlehčován tíhovou silou odpovídající 28 gramům. Od toho odečteme 4 gramy, které váží hélium a zjistíme, že každý mol hélia v balónu unese 22 gramů zátěže.
Řekněme, že budeme chtít, aby celková hmotnost balónu i s užitečnou zátěží byla 1 tuna. Vydělíme jednu tunu 22-mi gramy a zjistíme kolik molů hélia budeme potřebovat. Vyjde nám 45 500 molů hélia.
Mimochodem; doufám, že ještě stačíte sledovat. :-)
Jak velký bude balón
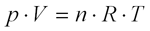
Když jsme zjistili, jaké množství atomů hélia budeme potřebovat, chceme také vědět, jak velký bude plyn zaujímat objem. Vyjdeme ze stavové rovnice pro ideální plyn. Ta říká, že součin objemu a tlaku plynu je roven součinu počtu molů molekul plynu, teploty v kelvinech a plynové konstanty. Objem chceme zjistit a počet molů známe. Ještě nevíme, jaký je v 60-ti kilometrech atmosférický tlak%20Mechanika%20kapalin%20a%20plynů.doc) (48kB doc – vypočet ze vzorce) a jaká je teplota. Teď už víme, že teplota se pohybuje kolem 0°C a tlak kolem 53 Pa.
Ze stavové rovnice vyjádříme objem a prostým dosazením nám vyjde, že plyn zabere přibližně 2 milióny metrů krychlových. Pokud si řekneme, že balón by měl mít tvar koule, což je z hlediska poměru povrchu k objemu nejlepší, tak by takový balón měl průměr 155 metrů.
To se zdá docela málo, že?
Kolik takový balón unese

měly průzkumné balóny
kulový tvar
Balón musí být z něčeho “ušitý” a to něco má také nějakou hmotnost. Vezměme si povrch našeho teoretického balónu a zjistěme, kolik by vážil metr čtverečný látky, kdyby měl unést jen sám sebe – tzn. nenesl by žádnou užitečnou zátěž. Prostě jednu tunu vydělíme povrchem balónu. V našem případě by to bylo přibližně 13 g/m2.
Metr čtverečný obyčejného kancelářského papíru važí 80 gramů. Mylarové fólie o potřebné i nižší hustotě existují, ale jejich pevnost je malá. Stačila by malá trhlinka a celý balón by se roztrhnul.
Takže jsme došli k závěru, že náš teoretický jednotunový kulový héliový balón bude rád, když ve výšce 60 km unese sám sebe.
Kde může být chyba

pro dosažení výšky 60 km
Credit: JP Aerospace
Přece se tím nebudou seriózně zabývat, když jednoduchým výpočtem mohli zjistit, že jim to fungovat nebude. Jediná věc, která by mohla tento nápad zachránit, je, že by balón byl skutečně hodně velký. Tím by se vylepšil poměr mezi objemem balónu a jeho povrchem. Ale vzhledem k tomu, že plánovaný tvar balónu je válcovitý, musel být až nesmyslně velký.
Cestování balónem do vesmíru je nesmysl!
Firma JP Aerospace nepochybně ví, co dělá, když uveřejnila takovou zprávu. Chce pouze získat popularitu a zájem veřejnosti. A to se jí daří. Takové balóny mohou doletět do 30 až 40 km, ale odtud je do opravdového vesmíru stále daleko.
A co z toho všeho plyne?
Nevěřte všemu, co píšou v novinách a když vás to zaujme, tak si to ověřte. Téměř vždy si vystačíte se znalostmi ze střední školy. *[mol]: 6,022.10²3 čehokoliv
Jirka Kouba – WWW – 3.6.2004
Dalibor Šrámek – WWW – 3.6.2004
Martin – WWW – 3.6.2004
Véna Maixner – 4.6.2004
fikus – 7.6.2004
Jan Vaněk jr. – WWW – 10.6.2004
Martin – WWW – 10.6.2004
Roj – WWW – 16.1.2006
Martin – WWW – 16.1.2006
Venca – 4.3.2012